Security Data Pipelines, Made Easy
Monad normalizes, filters, enriches, and routes your security data — cutting SIEM costs and freeing teams to focus on security.
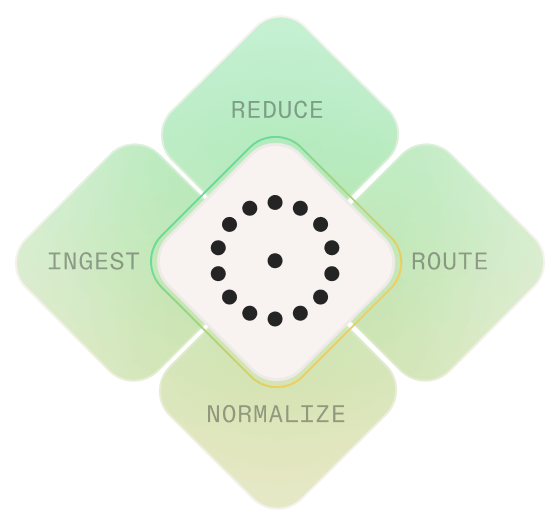
How Monad Works
Managed Data Pipelines
Connect any security tool in minutes. No custom parsers. No engineering toil. No BS.
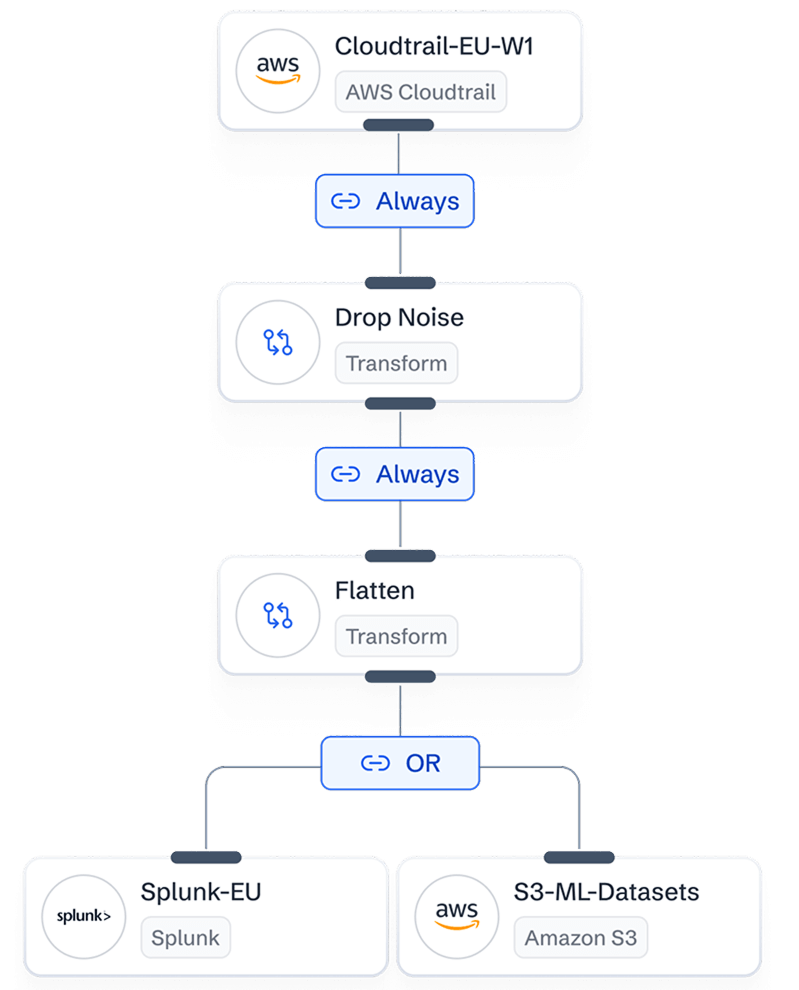
In-flight Data Transforms
Kill the noise before it costs you money. Filtering can strip out up to 70% of worthless data, keeping only what actually matters to your teams.
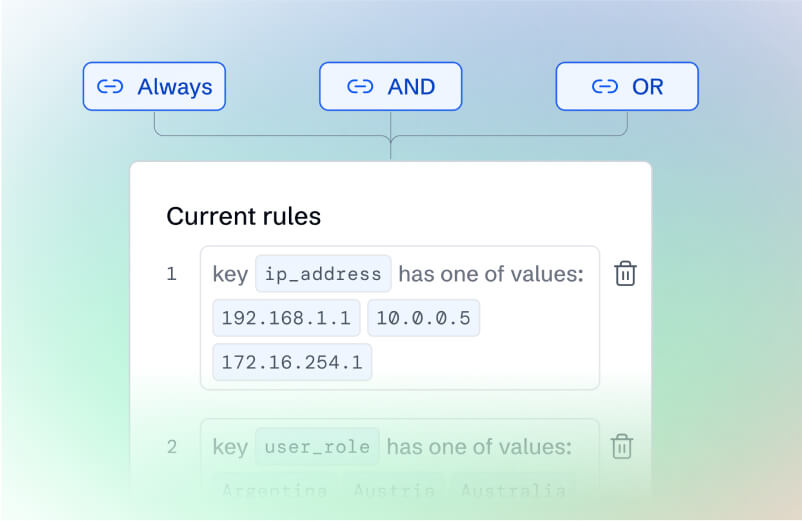
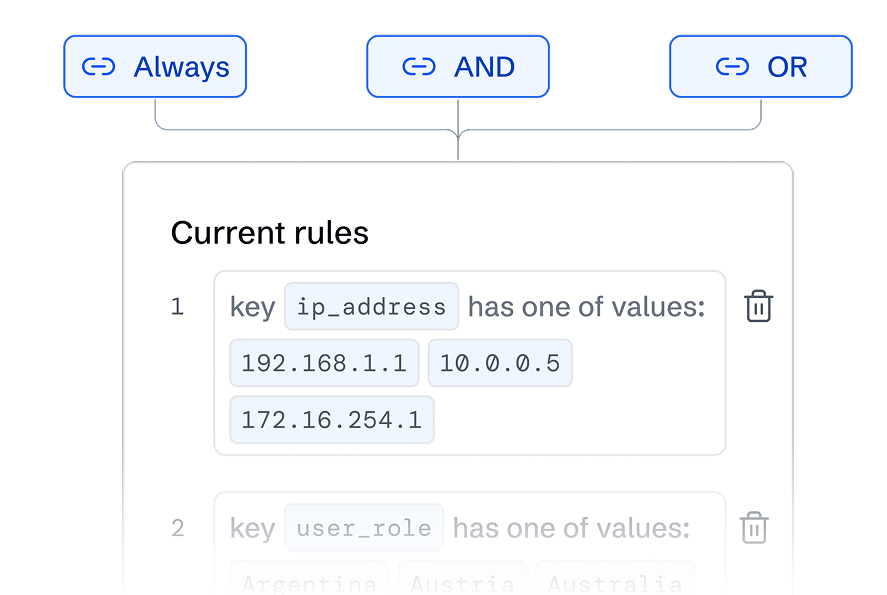
Rule-Based Data Routing
Send data where it delivers value. Intelligent routing puts high-value logs in your SIEM and archives the rest—cutting costs without losing visibility.
Deploy Your Way
Run it wherever makes sense for your security team. SaaS for simplicity, on-prem for control, hybrid for flexibility. Same powerful platform, your choice of deployment.

Why Teams Choose Monad
Cost Optimization at Every Step
Stop paying to store worthless telemetry. Smart filtering kills noise before it hits expensive storage. Less noise, lower bills, more budget for actual security tools.
Onboard in Minutes
No professional services. No implementation consultants. No 6-month deployments. Connect your first data source and see results before your coffee gets cold.
Developer-friendly ETL
Real APIs. Real SDKs. Real docs. Use Python, Go, or our REST API—whatever works for you. No proprietary languages or vendor lock-in tactics.
Scalability on Demand
Handle 10x log spikes without breaking a sweat. No capacity planning. No performance tuning. No emergency calls. Your data pipelines just work.
.png)